Algoritma - Binary Search

Binary Search

Bayangkan kamu ingin mencari sebuah kata dengan awalan huruf N di dalam sebuah kamus. Apa yang akan kamu lakukan? Kamu bisa saja menelusuri halaman per halaman sampai menemukan kata dengan awalan huruf N, tapi itu melelahkan dan membutuhkan waktu lama bukan?

Alih-alih membuka halaman per halaman, kamu akan memulainya dari halaman tengah sebuah kamus, lalu menyesuaikan kembali sampai bertemu kata dengan awalan huruf N. Yang kamu lakukan diatas adalah seperti algoritma binary search.

Binary Search adalah algoritma dalam dunia komputer yang fungsinya adalah menyelesaikan masalah pencarian dan dapat beroperasi/digunakan pada daftar/data yang sudah berurut.

Simple Search & Binary Search

Misalkan kita mencari angka 2 di dalam sebuah angka yang terurut dari -5 hingga 5.

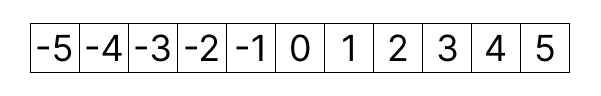
Kita bisa menelusuri satu per satu dimulai dari -5, -4, -3, -2 dan seterusnya.

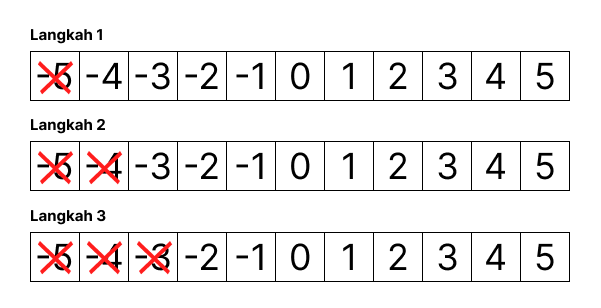
Ada 8 langkah yang harus kita lakukan untuk sampai mencari ke angka 2. Hal ini tidak efisien, bayangkan jika angkanya hingga 1000 dan kita mencari angka 850. Kita perlu melakukan 850 langkah untuk melakukannya. Inilah yang disebut dengan simple search (ada yang menyebutnya stupid search)

Cara yang lebih baik adalah menggunakan Binary Search

Cara Binary Search

Kita bisa memulainya dari nilai tengah.

n = 11
low = indeks ke-0 (-5)
high = indeks ke-n (5)
middle = (index low + index high) / 2

middle = (0 + 11) / 2 = 5 (0)

Artinya middle kita ada di index ke-5

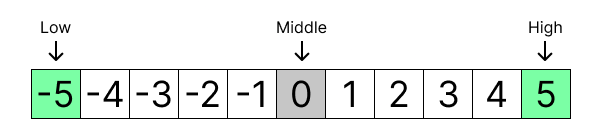
Apakah nilai middle sesuai yang kita cari? Tidak, ternyata terlalu rendah (0 < 2) Karena ternyata terlalu rendah, maka kita harus ubah index low = middle + 1

Kita ubah nilai

low = index middle + 1
low = 5 + 1 = 6

low = index ke-6 (1)

middle = (index low + index high) /2
middle = (6 / 11) / 2 = 8

middle = index ke-8 (3)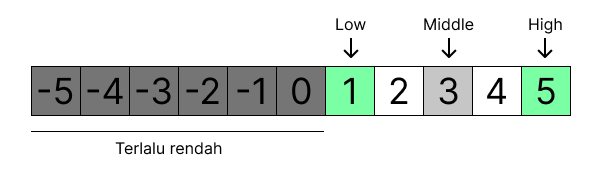

Nilai middle = 3, ternyata terlalu tinggi (3 > 2)

Karena ternyata terlalu tinggi, maka kita perlu mengubah index top = middle - 1

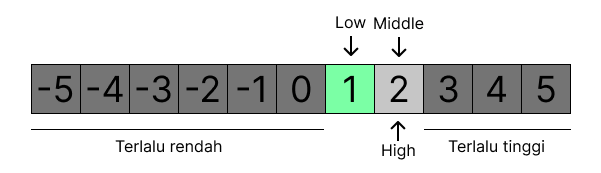
Sekarang middle = 1, lebih rendah dari apa yang kita cari (1 < 2)

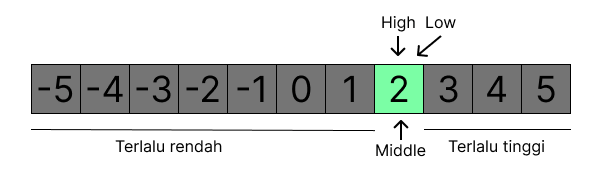
Maka kita perlu mengubah index low = middle + 1, jadi low, middle, top mengacu ke satu nilai yaitu 2, dan sudah sesuai dengan yang kita cari.

Perbandingan & Big O Notation

Simple Search membutuhkan 8 langkah sedangkan Binary Search membutuhkan 3 langkah.

Jika kita coba hitung menggunakan Big O Notation:

Simple Search:

10 data = 10 langkah
100 data = 100 langkah

Big O: O(n)

Binary Search:

10 data = 3 langkah
100 data = 7 langkah

Big O: O(log n)

Implementasi Kode

Kita coba implementasi menjadi bentuk kode Golang

package main

import "fmt"

func binarySearch(arr []int, target int) int {
	low := 0
	top := len(arr) - 1

	for low <= top {
		mid := low + (top-low)/2

		// Cek apakah nilai mid adalah target
		if arr[mid] == target {
			return mid
		} else if arr[mid] < target { // Jika target lebih besar dari mid, abaikan nilai yang lebih kecil
			low = mid + 1
		} else { // Jika target lebih kecil dari mid, abaikan nilai yang lebih besar
			top = mid - 1
		}
	}

	// Return -1 (tidak ada) jika nilai yang dicari tidak ditemukan
	return -1
}

func main() {
	arr := []int{-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5}
	target := 2

	index := binarySearch(arr, target)

	if index != -1 {
		fmt.Printf("Found %d at index %d\n", target, index)
	} else {
		fmt.Printf("%d not found in array\n", target)
	}
}